Giới thiệu
Tôi đã từng có một thời gian dài làm việc trong lĩnh vực tìm và phát hiện lỗ hổng phần mềm, cái nghề được gọi với cái tên khá lạ tai: vulnerability researcher. Công việc này đòi hỏi khá nhiều kỹ năng máy tính chuyên sâu. Trong bài viết này, tôi sẽ mô tả cách tôi sử dụng toán để tối ưu các testcase khi nghiên cứu các lỗ hổng. Tôi đã ứng dụng thuật toán này trong khá nhiều case khác nhau, đặc biệt là khi tôi phát hiện lỗ hổng CVE-2019-1208 | VBScript Remote Code Execution Vulnerability.
Cần lưu ý rằng:
- Tôi có một hệ thống sinh testcase tự động với thuật toán khá đặc biệt của tôi. Tôi sẽ không trình bày nó ở đây.
- Khái niệm đoạn mã có thể bao gồm 1 dòng cho tới k dòng.
- Thuật toán này sinh ra các đoạn mã có xác suất gây lỗi cho chương trình.
- Các đoạn mã sinh ra không phụ thuộc vào nhau. Xác suất một dòng code gây lỗi (crash) độc lập với các dòng khác. Đây là điều kiện quan trọng.
Vấn đề gặp phải
Trong quá trình tìm và phân tích mã, tôi gặp các vấn đề như sau:
- Số lượng testcase: Con số này không phải là 1 hoặc 2 để tôi có thể làm bằng tay.
- Thời gian thực thi 1 testcase lâu.
- Thời gian phân tích 1 testcase rất lâu khi phân tích bằng tay.
- Kích thước một testcase lớn (≈ hàng nghìn đoạn mã)
Tôi biết chắc chắn đã tìm ra lỗ hổng nhưng
- Cụ thể là đoạn mã nào gây lỗi thì tôi không thể biết.
- Tôi hạn chế về mặt thời gian do tôi phải thực hiện dự án khác của công ty, không thể để 100% thời gian cho lỗ hổng này.
- Tôi phải chạy đua với các researcher khác.
Tôi mong muốn có 1 hệ thống:
- Tự động sinh testcase và tìm lỗi (Đã có)
- Tự động tối ưu testcase và phân tích lỗi (Cần xây dựng)
- Tự động phân tích lỗi, điền form cần thiết, đánh giá các khả năng khai thác và độ nguy hiểm.
Dựa vào tất cả các mong muốn trên, tôi nghĩ đến một phương pháp để tối ưu testcase tự động, tốc độ cao và chính xác. Tôi nhớ đến các bài toán về xác suất đã được dạy khi đi học.
Một số điểm cần lưu ý:
- Xác định 2 testcase trùng nhau
- Xác định số tối ưu khi thực hiện.
Các testcase được tính là trùng nhau khi:
- Trạng thái crash tại cùng địa chỉ EIP/RIP
- Trạng thái Stack của chương trình khi crash trùng nhau
- Một số giá trị của thanh ghi trùng nhau
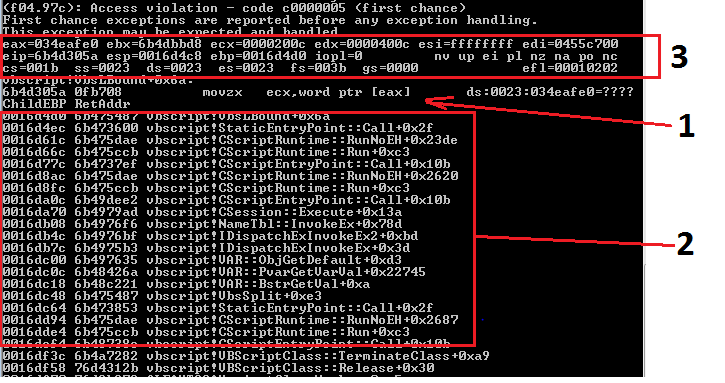
Giả sử: Các đoạn code không có sự liên hệ với nhau trong quá trình thực thi
Nên: Xác suất một đoạn code gây crash độc lập với các đoạn khác.
Đây là giả thiết của tôi. Giả thiết này của tôi luôn đúng do tôi tự sinh các testcase và kiểm soát được đầu ra của chúng.
Ta có phương pháp tối ưu testcase đơn giản, thông qua 3 bước sau:
- Xóa bỏ lần lượt các đoạn trong testcase ban đầu nhằm sinh testcase mới
- Test thử với chương trình
- Chỉ giữ lại các testcase có kích thước nhỏ, trùng với testcase ban đầu
Cần phải xóa bao nhiêu đoạn trong testcase?
- Số đoạn xóa đi phải đủ nhỏ để xác suất có testcase trùng là cao nhất. Hiển nhiên rằng nếu các bạn xóa càng ít đoạn, thì xác suất xóa phải đoạn không liên quan càng cao, testcase càng có xác suất lớn để trùng.
- Số đoạn xóa đi phải đủ lớn để giảm thời gian tối ưu. Hiển nhiên rằng nếu càng xóa nhiều đoạn, testcase càng nhỏ.
Con số bao nhiêu là hợp lý????
Giả sử cắt bỏ x đoạn mã trong testcase ban đầu (có N đoạn mã):
Xác suất để cắt bỏ 1 đoạn mã nhưng vẫn được testcase trùng ≈ 100%
Xác suất cắt bỏ đoạn mã thứ 2 nhưng vẫn được testcase trùng (1 – 1/N)
Xác suất cắt bỏ đoạn mã thứ 3 nhưng vẫn được testcase trùng (1 – 2/N)
…
Xác suất cắt bỏ đoạn mã thứ x nhưng vẫn được testcase trùng (1 – (x-1)/N)
Xác suất để cắt bỏ x đoạn mã nhưng vẫn được testcase trùng
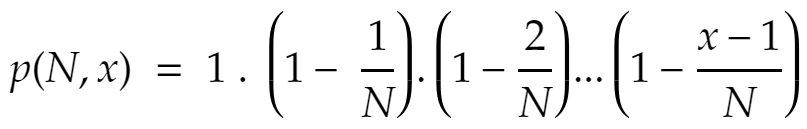
Rõ ràng, đây là một phương trình khá khó giải và tôi cũng không phải người giỏi toán để đưa ra đáp án chính xác. Chúng ta lại dùng các công thức ước lượng được mô tả trong sách giáo khoa: Công thức xấp xỉ Taylor
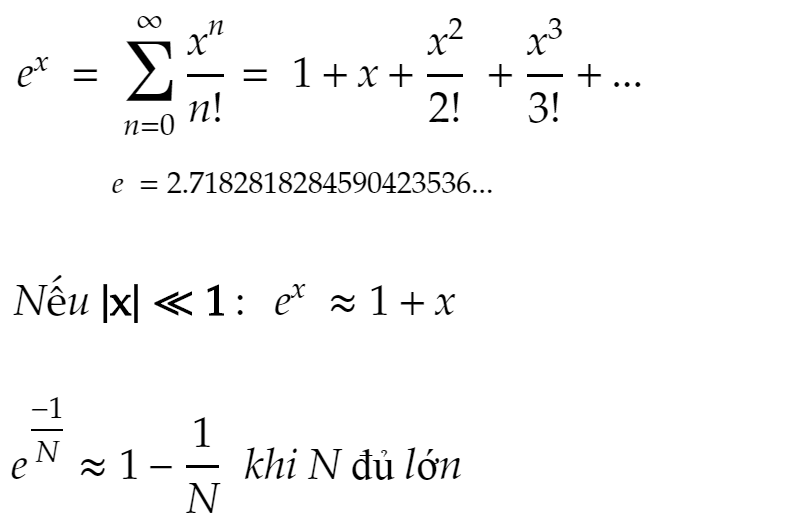
Tiếp tục:
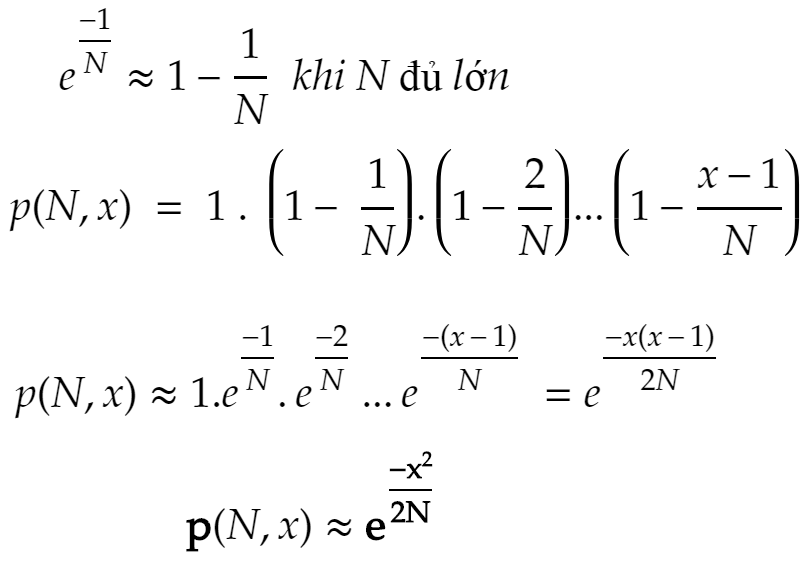
Nói cách khác, với N là số đoạn code, p là xác suất được lựa chọn, thì chúng ta có x là số đoạn code cần chọn ngẫu nhiên để testcase mới trùng với testcase cũ.
Nếu chúng ta giả định p = 0.5 = 50%, thay thế vào công thức tính xác suất ban đầu, ta có được công thức cuối cùng:
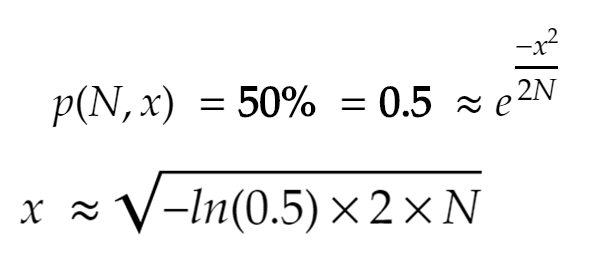
hay nói cách khác, x xấp xỉ bằng 1.17741*sqrt(N), có thể coi là sqrt(N).
Như vậy, nếu chúng ta cắt đi sqrt(N) đoạn mã trong N đoạn mã, thì xác suất xảy ra testcase trùng sẽ lớn hơn 50%. Độ phức tạp thuật toán là O(n). Do số lượng đoạn được cắt đi lớn khi N lớn, tốc độ hội tụ của thuật toán này được cải thiện đáng kể so với việc tối ưu tuần tự. Một kết luận rất ngắn và đơn giản phải không?
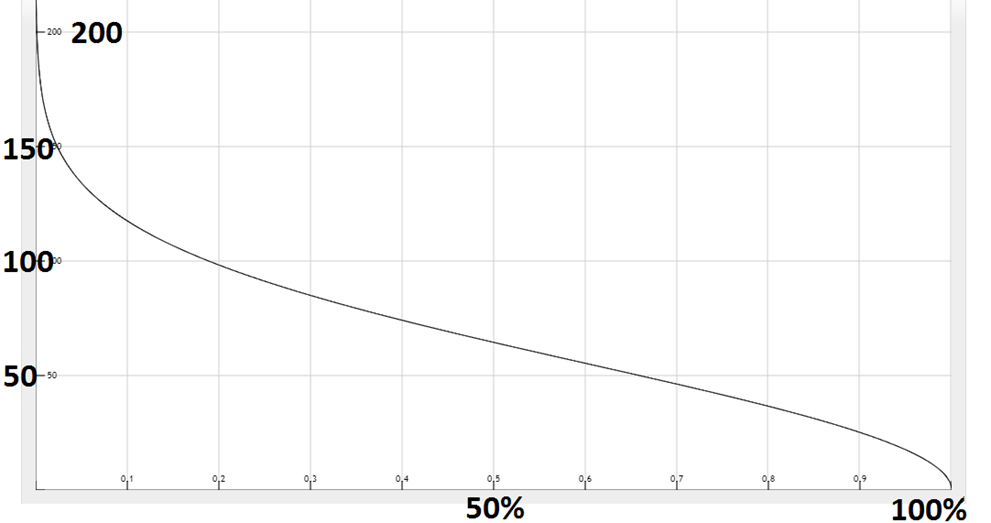
Nếu chúng ta chọn N là 3000 đoạn mã.
Trục Y là số đoạn mã được loại bỏ.
Trục X là xác suất xảy ra trùng nhau
Kết luận
Qua bài viết vừa rồi, tôi hy vọng rằng các bạn có thể có cái nhìn sâu sắc hơn với môn toán cũng như phương pháp ứng dụng các bài toán “ngày xửa ngày xưa” vào các vấn đề trong công việc hiện tại. Nét đẹp của toán học sẽ chỉ phát huy khi chúng được đặt vào đúng tình huống cụ thể. Đừng để các bài toán của các bạn chỉ nằm trên giấy./.
